Periodic Trends of the Transition Metals

Periodic trends play a huge role in organic chemistry. Regular changes in electronegativity, atomic size, ionization energy, and other variables across the periodic table allow us to make systematic predictions about the behavior of similar compounds. Of course, the same is true for organometallic complexes! With a firm grip on the periodic trends of the transition metals, we can begin to make comparisons between complexes we’re familiar with and those we’ve never seen before. Periodic trends essentially provide an exponential increase in predictive power. In this post, we’ll hit on the major periodic trends of the transition metals and discuss a few examples for which these trends can be handy.

Before beginning, a couple of caveats are in order. First of all, many of the trends across the transition series are not perfectly regular. Hartwig wisely advises that one should consider the transition series in blocks instead of as a whole when considering periodic trends. For instance, general increases in a quantity may be punctuated by sudden decreases; in such a case, we may say that the quantity increases generally, but definite conclusions are only possible when the metals under comparison are close to one another in the periodic table (and we need to be careful about unexpected jumps). Secondly, periodic trends are significantly affected by the identity of ligands and the oxidation state of the metal center, so comparisons need to be appropriately controlled. Using periodic trends to compare a Pd(II) complex and a Ru(III) complex is largely an exercise in futility, but comparing Pt(II) and Pd(II) complexes with similar ligand sets is reasonable. Keep these ideas in mind to avoid spinning your wheels unnecessarily! Alright, let’s dive in…

Atomic Size

Trends in atomic size are probably the most straightforward of the transition series. The figure below shows the covalent radii of metals in groups 4-10. Covalent radius is a convenient metric for atomic size, particularly since we’re interested in the size of metals in OM complexes. Please note that the row numbers below are referenced to the transition series only, not the periodic table as a whole.

Covalent radius as a function of group and row number. Note the odd transition from row 2 to 3!

Even this graph holds some mystery, but let’s begin with what jumps out:

• As we move across the periodic table from left to right, covalent radius decreases.
• As we move down a group (from row 1 to 2), covalent radius increases.

The down-a-group trend makes sense for the simple reason that principal quantum number increases as we move down a group. Does the previous sentence look like gibberish to you? (You might be an organic chemist if…) Just remember this: orbitals get larger as we move down a group. It’s as true for the transition metals as it is for the rest of the periodic table. As for the left-to-right trend, this too has a straightforward explanation. As we move to the right across the periodic table protons are added to the nucleus, but the added electrons don’t exactly balance the proton’s charge (because of shielding). The net result is that effective nuclear charge increases as we move left-to-right across the periodic table. There are two important consequences of this phenomenon: electronegativity increases and size decreases as we move left to right. The same trend is observed for carbon, nitrogen, oxygen, and fluorine.

There is still something amiss: the third-row metals are just about the same size as the second-row metals, particularly as we move toward the late metals. What gives?! You can’t explain that…it certainly seems inconsistent with our previous discussion about larger orbitals as we move down a group. Actually, Mr. O’Reilly, we can explain it—and we don’t really need to invoke anything new to do so. The lanthanides jammed between rows 2 and 3 of the transition series are the key. From row 2 to 3, orbitals do get larger due to an increase in principal quantum number, but this effect is counterbalanced by a large horizontal walk across the lanthanides before we reach the third row of the transition series. The ultimate result is that the third-row transition metals are roughly the same size as their second-row counterparts.

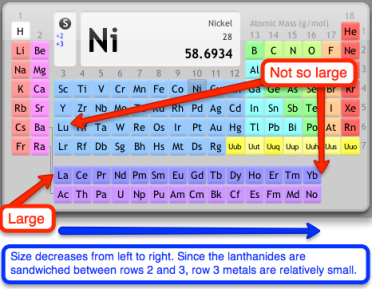
The third-row transition metals possess relatively small covalent radii due to the "lanthanide contraction."

The significant difference in size between first- and second-row metals has been exploited in a number of cases, and we will see it again. A famous example is asymmetric nickel-catalyzed alpha-arylation, which exhibits higher enantioselectivity than palladium-catalyzed methods. The higher stereoselectivity of the nickel catalyst is attributed to the smaller nickel center. Or, if you want to sound like the pros, the “more intimate chiral environment” of nickel catalysts.

Ionization Energy

A transition metal’s ionization energy is related to the energies of its d orbitals, its ease of oxidation, and its basicity. In simplest terms, the greater a metal’s ionization energy, the harder it is to pull an electron from it. Thus, metal centers with high ionization energies exhibit low basicity (or nucleophilicity) and are resistant to oxidation. Trends in ionization energy are more complex than atomic size trends, as the plot below amply demonstrates.

What order can we pull from this chaos of ionization energies?

The first thing we may notice is that in general, ionization energy increases as we move from left to right across a row. Notable dips occur at row 1, group 10 (Ni) and row 3, group 7 (Re). However, the general trend is consistent with our previous notion that electronegativity increases as we move left-to-right across a row. As for trends down a group, it’s difficult to discern anything useful in the graph above. What we can say (considering second and higher ionization potentials, not shown) is that higher oxidation states are more accessible to third-row metals. Easy way to remember this: OsO₄ is a stable reagent that reacts only with alkenes; RuO₄ is prepared in situ and ravages alkenes and alcohols; FeO₄ has never been observed.

We’ll touch on trends in acidity/basicity again in a later post on hydride ligands, but they tend to follow the trends in bond strength described below: basicity increases (and acidity decreases) as we move down a group, generally.

Bond Strengths

The strengths of metal–main group bonds in organometallic complexes vary in somewhat predictable ways. In general, bond strengths increase moving down a group. Believe it or not, this trend is not that surprising in light of the trends in ionization energies we’ve already discussed. Large ionization energy suggests low-energy d orbitals, and lower-energy d orbitals are better matched for overlap with the orbitals of the organic elements. We should thus expect stronger bonds to be associated with higher ionization energies…and that’s what’s observed, in general! This is largely a covalent argument, to the extent that it rests on orbital overlap ideas; ionic effects related to partial charges are also important, but we won’t open that can of worms here.

Summary

Here’s a handy bulleted list of the general trends discussed in this post. USE WITH CARE!

• As we move across the periodic table from left to right, covalent radius decreases.
• As we move down a group (from row 1 to 2), covalent radius increases. Corresponding second- and third-row metals are roughly the same size.
• As we move across the periodic table from left to right, ionization energy and electronegativity increase.
• As we move down a group, high oxidation states become more accessible.
• As we move down a group, basicity increases and acidity decreases.
• As we move down a group, metal–main group bond strengths increase.