Epic Ligand Survey: π Systems (Part 1)

With this post, we finally reach our first class of dative actor ligands, π systems. In contrast to the spectator L-type ligands we’ve seen so far, π systems most often play an important role in the reactivity of the OM complexes of which they are a part (since they act in reactions, they’re called “actors”). π Systems do useful chemistry, not just with the metal center, but also with other ligands and external reagents. Thus, in addition to thinking about how π systems affect the steric and electronic properties of the metal center, we need to start considering the metal’s effect on the ligand and how we might expect the ligand to behave as an active participant in reactions. To the extent that structure determines reactivity—a commonly repeated, and extremely powerful maxim in organic chemistry—we can think about possibilities for chemical change without knowing the elementary steps of organometallic chemistry in detail yet. And we’re off!

General Properties

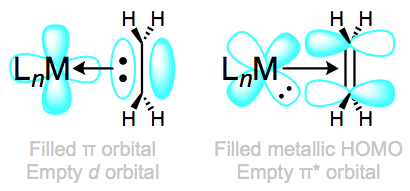
The π bonding orbitals of alkenes, alkynes, carbonyls, and other unsaturated compounds may overlap with d_σ orbitals on metal centers. This is the classic ligand HOMO → metal LUMO interaction that we’ve beaten into the ground over the last few posts. Because of this electron donation from the π system to the metal center, coordinated π systems often act electrophilic, even if the starting alkene was nucleophilic (the Wacker oxidation is a classic example; water attacks a palladium-coordinated alkene). The  π → d_σ orbital interaction is central to the structure and reactivity of π-system complexes.

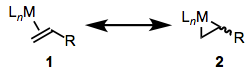
Then again, a theme of the last three posts has been the importance of orbital interactions with the opposite sense: metal HOMO → ligand LUMO. Like CO, phosphines, and NHCs, π systems are often subject to important backbonding interactions. We’ll focus on alkenes here, but these same ideas apply to carbonyls, alkynes, and other unsaturated ligands bound through their π clouds. For alkene ligands, the relative importance of “normal” bonding and backbonding is nicely captured by the relative importance of the two resonance structures in the figure below.

Resonance forms of alkene ligands.

Complexes of weakly backbonding metals, such as the electronegative late metals, are best represented by the traditional dative resonance structure 1. But complexes of strong backbonders, such as electropositive Ti(II), are often best drawn in the metallacyclopropane form 2. Organic hardliners may have a tough time believing that 1 and 2 are truly resonance forms, but several studies—e.g. of the Kulinkovich cyclopropanation—have shown that independent synthetic routes to metallacyclopropanes and alkene complexes containing the same atoms result in the same compound. Furthermore, bond lengths and angles in the alkene change substantially upon coordination to a strongly backbonding metal. We see an elongation of the C=C bond (consistent with decreased bond order) and some pyramidalization of the alkene carbons (consistent with a change in hybridization from sp² to sp³). A complete orbital picture of “normal” bonding and backbonding in alkenes is shown in the figure below.

Normal bonding and backbonding in alkene complexes.

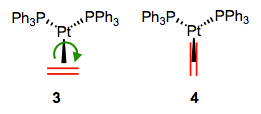
Here’s an interesting question with stereochemical implications: what is the orientation of the alkene relative to the other ligands? From what we’ve discussed so far, we can surmise that one face of the alkene must point toward the metal center. Put differently, the bonding axis must be normal to the plane of the alkene. However, this restriction says nothing about rotation about the bonding axis, which spins the alkene ligand like a pinwheel. Is a particular orientation preferred, or can we think about the alkene as a circular smudge over time? The figure below depicts two possible orientations of the alkene ligand in a trigonal planar complex. Other orientations make less sense because they would involve inefficient orbital overlap with the metal’s orthogonal d orbitals. Which one is favored?

Two limiting cases for alkene orientation in a trigonal planar complex.

First of all, we need to notice that these two complexes are diastereomeric. They have different energies as a result, so one must be favored over the other. Naive steric considerations suggest that complex 4 ought to be more stable (in most complexes, steric factors dictate alkene orientation). To dig a little deeper, let’s consider any electronic factors that may influence the preferred geometry. We’ve already seen that electronic factors can overcome steric considerations when it comes to complex geometry! To begin, we need to consider the crystal field orbitals of the complex as a whole. Verify on your own that in this d¹⁰, Pt(0) complex, the crystal-field HOMOs are the d_xy and d_x²–y² orbitals. Where are these orbitals located in space? In the xy-plane! Only the alkene in 3 can engage in efficient backbonding with the metal center. In cases when the metal is electron rich and/or the alkene is electron poor, complexes like 3 can sometimes be favored in spite of sterics. The thought process here is very similar to the one developed in an earlier post on geometry. However, please note that this situation is fairly rare—steric considerations often either match or dominate electronics where alkenes are concerned.

Synthesis

Alkene and alkyne complexes are most often made via ligand substitution reactions, which simply exchange one ligand for another. A nice example of a stable alkene complex synthesized via ligand substitution is [Ir(COD)Cl]₂, made from IrCl₃ and cyclooctadiene. Similarly, the inimitable Pd₂(dba)₃ may be prepared from PdCl₄^2– and dibenzylideneacetone (dba). In truth, only a few stable alkene and alkyne complexes find use as organometallic precatalysts and/or catalysts. Substitutions of alkenes for phosphine ligands can be rendered easy, so phosphine precatalysts may be used in reactions that involve intermediate alkene complexes. In addition, unsaturated complexes containing an open coordination site often associate with alkenes and alkynes. Gold(I) chemistry is riddled with examples of this strategy, for example. The unsaturated complexes may be derived from precursors themselves, and the resulting π complexes may be short lived, but that’s often the point! Some transformation of the π system is often desired.

I have to mention the metallacyclopropane route to alkene complexes from the Kulinkovich reaction, which is a surprising but awesome transformation. After displacement of two alkoxide ligands on titanium by ethylmagnesium bromide, a process described as either (1) β-hydride elimination followed by reductive elimination, or (2) concerted σ-bond metathesis leads to the liberation of ethane and formation of the alkene complex. The proof that the product is an alkene complex? Other olefins can displace ethylene, and ethylene can come right back in to re-form the product! Ti(II)’s strong backbonding ability almost certainly figures in to the driving force for the ethane-releasing step(s).

Kulinkovich synthesis of alkene complexes. A remarkable loss of ethane!

Reactions

The reactivity patterns of alkene and alkyne ligands are remarkably similar to those of carbon monoxide: nucleophilic attack and migratory insertion dominate their chemistry. The important issues of site selectivity and stereoselectivity come into play when considering alkenes and alkynes, however—the fundamental questions are…

• Which atom gets the nucleophile/migrating group?
• Which atom gets the metal?
• What is the relative orientation of the nucleophile/migrating group and the metal (cis or trans)?

The wide variety of what we might generally call “atom-metallation” processes (carbopalladation, carboauration, aminopalladation, oxypalladation, etc.) may involve external nucleophilic addition to the π system, with attachment of the metal to the carbon that was not attacked. The net result is the addition of atom and metal across the π bond, in a trans or anti orientation. The anti orientation results because the nucleophile attacks the face opposite the metal center. A cis orientation of nucleophile and metal is indicative of a migratory insertion pathway (see below). In the example in the following figure, the metal alkyl was converted into a chlorohydrin using copper(II) chloride and LiCl (with stereospecific inversion). Subsequent epoxide formation with NaOH afforded only the cis diastereomer, supporting the trans configuration of the metal alkyl.

Nucleophilic attack on a coordinated alkene or alkyne is always trans, or anti.

Migratory insertion of alkenes and alkynes, like insertions of CO, can be thought of as an internal attack by a nucleophile already coordinated to the metal center. Migratory insertion is the C–C bond-forming step of olefin polymerization, and some fascinating studies of this reaction have shown that the alkyl group (the growing polymer chain) migrates to the location of the olefin (not the other way around). Migratory insertion is also important for the Heck reaction—in this case, the olefin inserts into a Pd–C_sp² bond. Finally, a large number of metal-catalyzed addition reactions rely on migratory insertion as the key C–X bond-forming step. cis-Aminopalladation is one example.

cis-Aminopalladation via migratory insertion. Two new bonds are established with stereospecificity!

Importantly, migratory insertion of alkenes and alkynes into M–X bonds takes place in a syn or cis fashion—the metal and the migrating group (X) end up on the same face of the π system. The site selectivity of migratory insertion may be controlled by either steric factors or the π system’s electronics, although the former is more common, I’d say. Electronics are at play in Wacker oxidations of 1-alkenes, for example, which exclusively yield methyl ketones.

Finally, electrophilic attack on π systems coordinated to electron-rich metals can also happen, although it’s much rarer than nucleophilic attack. Usually these reactions involve coordination of the electrophile to the metal, followed by migratory insertion. We’ll hear more about this in a future post on electrophilic attack on coordinated ligands. Coming up next: cyclic π systems!