Reductive Elimination: General Ideas

Reductive elimination is the microscopic reverse of oxidative addition. It is literally oxidative addition run in reverse—oxidative addition backwards in time! My favorite analogy for microscopic reversibility is the video game Braid, in which “resurrection is the microscopic reverse of death.” The player can reverse time to “undo” death; viewed from the forward direction, “undoing death” is better called “resurrection.” Chemically, reductive elimination and oxidative addition share the same reaction coordinate. The only difference between their reaction coordinate diagrams relates to what we call “reactants” and “products.” Thus, their mechanisms depend on one another, and trends in the speed and extent of oxidative additions correspond to opposite trends in reductive eliminations. In this post, we’ll address reductive elimination in a general sense, as we did for oxidative addition in a previous post.

A general reductive elimination. The oxidation state of the metal decreases by two units, and open coordination sites become available.

During reductive elimination, the electrons in the M–X bond head toward ligand Y, and the electrons in M–Y head to the metal. The eliminating ligands are always X-type! On the whole, the oxidation state of the metal decreases by two units, two new open coordination sites become available, and an X–Y bond forms. What does the change in oxidation state suggest about changes in electron density at the metal? As suggested by the name “reductive,” the metal gains electrons. The ligands lose electrons as the new X–Y bond cannot possibly be polarized to both X and Y, as the original M–X and M–Y bonds were. Using these ideas, you may already be thinking about reactivity trends in reductive elimination…hold that thought.

Epic Ligand Survey: Odd-numbered π Systems

Odd-numbered π systems—most notably, the allyl and cyclopentadienyl ligands—are formally L_nX-type ligands bound covalently through one atom (the “odd man out”) and datively through the others. This formal description is incomplete, however, as resonance structures reveal that multiple atoms within three- and five-atom π systems can be considered as covalently bound to the metal. To illustrate the plurality of equally important resonance structures for this class of ligands, we often just draw a curved line from one end of the π system to the other. Yet, even this form isn’t perfect, as it obscures the possibility that the datively bound atoms may dissociate from the metal center, forming σ-allyl or ring-slipped ligands. What do the odd-numbered π systems really look like, and how do they really behave? We’ll try to get to the bottom of these questions in the remainder of this post.

General Properties

Allyls are often actor ligands, most famously in allylic substitution reactions. The allyl ligand is an interesting beast because it may bind to metals in two ways. When its double bond does not become involved in binding to the metal, allyl is a simple X-type ligand bound covalently through one carbon—basically, a monodentate alkyl! Alternatively, allyl can act as a bidentate LX-type ligand, bound to the metal through all three conjugated atoms. The LX or “trihapto” form can be represented using one of two resonance forms, or (more common) the “toilet-bowl” form seen in the general figure above. I don’t like the toilet-bowl form despite its ubiquity, as it tends to obscure the important dynamic possibilities of the allyl ligand.

Can we use FMO theory to explain the wonky geometry of the allyl ligand?

The lower half of the figure above illustrates the slightly weird character of the geometry of allyl ligands. In a previous post on even-numbered π systems, we investigated the orientation of the ligand with respect to the metal and came to some logical conclusions by invoking FMO theory and backbonding. A similar treatment of the allyl ligand leads us to similar conclusions: the plane of the allyl ligand should be parallel to the xy-plane of the metal center and normal to the z-axis. In reality, the allyl plane is slightly canted to optimize orbital overlap—but we can see at the right of the figure above that π₂–d_xy orbital overlap is key. Also note the rotation of the anti hydrogens (anti to the central C–H, that is) toward the metal center to improve orbital overlap.

Epic Ligand Survey: π Systems (Part 1)

With this post, we finally reach our first class of dative actor ligands, π systems. In contrast to the spectator L-type ligands we’ve seen so far, π systems most often play an important role in the reactivity of the OM complexes of which they are a part (since they act in reactions, they’re called “actors”). π Systems do useful chemistry, not just with the metal center, but also with other ligands and external reagents. Thus, in addition to thinking about how π systems affect the steric and electronic properties of the metal center, we need to start considering the metal’s effect on the ligand and how we might expect the ligand to behave as an active participant in reactions. To the extent that structure determines reactivity—a commonly repeated, and extremely powerful maxim in organic chemistry—we can think about possibilities for chemical change without knowing the elementary steps of organometallic chemistry in detail yet. And we’re off!

General Properties

The π bonding orbitals of alkenes, alkynes, carbonyls, and other unsaturated compounds may overlap with d_σ orbitals on metal centers. This is the classic ligand HOMO → metal LUMO interaction that we’ve beaten into the ground over the last few posts. Because of this electron donation from the π system to the metal center, coordinated π systems often act electrophilic, even if the starting alkene was nucleophilic (the Wacker oxidation is a classic example; water attacks a palladium-coordinated alkene). The  π → d_σ orbital interaction is central to the structure and reactivity of π-system complexes.

Then again, a theme of the last three posts has been the importance of orbital interactions with the opposite sense: metal HOMO → ligand LUMO. Like CO, phosphines, and NHCs, π systems are often subject to important backbonding interactions. We’ll focus on alkenes here, but these same ideas apply to carbonyls, alkynes, and other unsaturated ligands bound through their π clouds. For alkene ligands, the relative importance of “normal” bonding and backbonding is nicely captured by the relative importance of the two resonance structures in the figure below.

Resonance forms of alkene ligands.

Gee, I’m a Tree: Predicting the Geometry of Organometallic Complexes

An important issue that we’ve glossed over until now concerns what organometallic complexes actually look like: what are their typical geometries? Can we use any of the “bookkeeping metrics” we’ve explored so far to reliably predict geometry? The answer to the latter questions is a refreshing but qualified “yes.” In this post, we’ll explore the possibilities for complex geometry and develop some general guidelines for predicting geometry. In the process we’ll enlist the aid of a powerful theoretical ally, crystal field theory (CFT). CFT provides some intuitive explanations for geometry the geometry of OM complexes. Here we go!

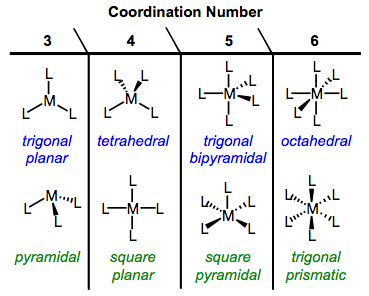
Because OM complexes feature a variety of coordination numbers, the possibilities for geometry are numerous. The common geometries of organic chemistry—linear, pyramidal, trigonal planar, and tetrahedral—are available to OM complexes too. Many complexes exhibit a second kind of four-coordinate geometry, square planar. Five-coordinate complexes may exhibit either square pyramidal or (my personal favorite) trigonal bipyramidal geometries. Six-coordinate complexes feature either octahedral geometry or the rare but intriguing trigonal prismatic arrangement. The figure below summarizes these possibilities (minus the two-coordinate geometries, which we won’t deal with).

Common geometries of organometallic complexes.

Simplifying the Organometallic Complex (Part 2)

Now it’s time to turn our attention to the metal center, and focus on what the deconstruction process can tell us about the nature of the metal in organometallic complexes. We’ll hold off on a description of periodic trends of the transition series, but now is a good time to introduce the general characteristics of the transition metals. Check out groups 3-12 in the table below.

The transition metals are colored dark blue in this table.

The transition metals occupy the d-block of the periodic table, meaning that, as we move from left to right across the transition series, electrons are added to the d atomic orbitals. Just like organic elements, the transition metals form bonds using only their valence electrons. But when working with the transition metals, we need to concern ourselves only with the d atomic orbitals, as none of the other valence subshells contain any electrons. Although the periodic table may lead you to believe that the transition metals possess filled s subshells, we imagine metals in organometallic complexes as possessing valence electrons in d orbitals only! The reason for this is somewhat complicated, but has to do with the partial positive charge of complexed metals. Neutral transition metal atoms do, in fact, possess filled s subshells. Why, then, is it important to remember that the valence electrons of complexed metal centers are all d electrons? We will see that the number of d electrons possessed by a complexed metal is in many ways a useful concept. If you find that your counts are off by two, this common mistake is probably the culprit!